그래프 자료구조에서 최단 경로, 최소 비용를 구해야 하는 알고리즘은
너비 우선 탐색(BFS), 다익스트라, 벨만-포드, 플로이드 워샬 이 있습니다.
1. 다익스트라(Dijkstra) 알고리즘 이란?
그래프 자료구조에서 노드와 가중치가 있는 간선이 존재하고,
시작 노드에서 모든 노드까지의 최단 경로(최소 비용)를 구하는 알고리즘 입니다.

위 그래프를 예시로 보자면, 1번 노드를 시작해서 다른 모든 노드(2, 3, 4, 5)까지의 최단 경로를 구해야 합니다. 그리고 각 노드를 잇는 간선(방향 존재 유무는 중요하지 않습니다. 갈 수 있냐, 없냐 차이 이므로!)에는 가중치가 있습니다. 이 그래프에서 노드1을 시작으로 다익스트라 알고리즘을 적용해 다른 노드까지의 최단 경로를 구해 보겠습니다.
2. 다익스트라 적용해보기
다익스트라 알고리즘에서는 시작 노드부터 점차 가중치를 더해 다른 노드로 방문하는 순서를 거치게 됩니다. 그러면서 각 노드를 방문했을 때 거쳐온 간선들의 가중치 최소 합을 메모리에 갱신해 줘야 합니다. 이 방문하는 프로세스를 조작하기 위해 "PriorityQueue" 자료구조와 가중치 값을 담을 "Array" 배열을 사용합니다. Priority Queue는 간선의 가중치를 보관하며 그 가중치 값이 작은 순으로 정렬하면서, 우선적으로 적은 가중치의 합을 먼저 구하기 위해 사용됩니다.

우선 각 노드까지 도달하는데 소요되는 간선의 가중치 값을 담는 배열을 선언해 줍니다.(여기서는 int Dijk[5]) 그리고 각 배열 값은 담을 수 있는 가장 큰 값(INF)으로 채워줍니다. 이 예시에서는 노드 1을 시작으로 정해, PriorityQueue(이하 PQ)에 담아 주고, Dijk[1] 값을 0으로 저장(시작 노드는 간선을 거쳐온 적이 없기 때문)해 줍니다.

PQ 맨 앞에 들어있는 노드를 가져오고 보니(동시에 PQ Pop 수행), 1번 노드가 들어 있네요. 이제 1번 노드에서 다음으로 갈 수 있는 노드는 몇번인가 탐색을 합니다. 여기서는 2번노드와 3번노드로 나아갈 수 있겠군요.

우선 8의 가중치를 소비하면서 2번 노드를 방문하게 됩니다. 이 때, Dijk[2]는 아주 큰 값인 "INF"가 저장되어 있고, 2번으로 움직이면서 가중치 8이라는 값이 INF보다 작게 되므로 2번 방문이 가능해짐과 동시에 8로 값을 갱신해 줍니다. 이후에 마지막으로 탐색한 2번 노드를 PQ에 Push해 줍니다.

다음으로 1번에서 갈 수 있는 3번 노드를 방문해 봅시다. 2번 노드를 방문할 때와 마찬가지로 Dijk[3]은 "INF"가 저장되어 있고 3번 노드로 이동하면서 가져온 가중치 2가 더 작기 때문에 3번 노드를 방문할 수 있습니다. 동시에 Dijk[3]도 2로 갱신하고 PQ에 3번 노드를 Push해 줍니다. 이 때, 원래 저장되어 있던 2보다 3이 더 큰 값이므로, PQ 정렬에 의해 노드 3이 가장 앞으로 정렬됩니다.

드디어 1번 노드에서 갈 수 있었던 2, 3번 노드를 방문하며 최소 가중치를 갱신했군요! 이 상태에서의 PQ와 Dijk 배열에 저장된 값을 확인해 보세요!
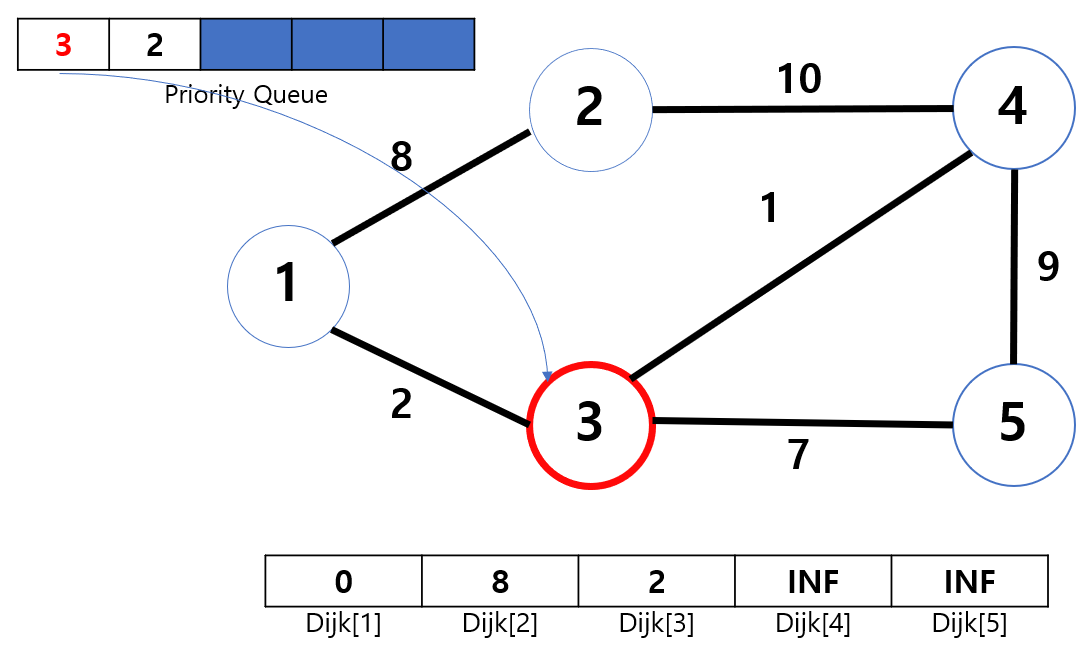
이제 1번 노드 탐색은 끝났으니, 다음 차례로 진행해 보죠. PQ에서 맨 앞에 있는 노드를 가져와 보니(동시에 PQ Pop 수행) 3번 노드가 있네요! 이제 3번 노드에서 갈 수 있는 노드는 무엇인지 탐색해 보니 1, 4, 5번 노드가 있습니다.
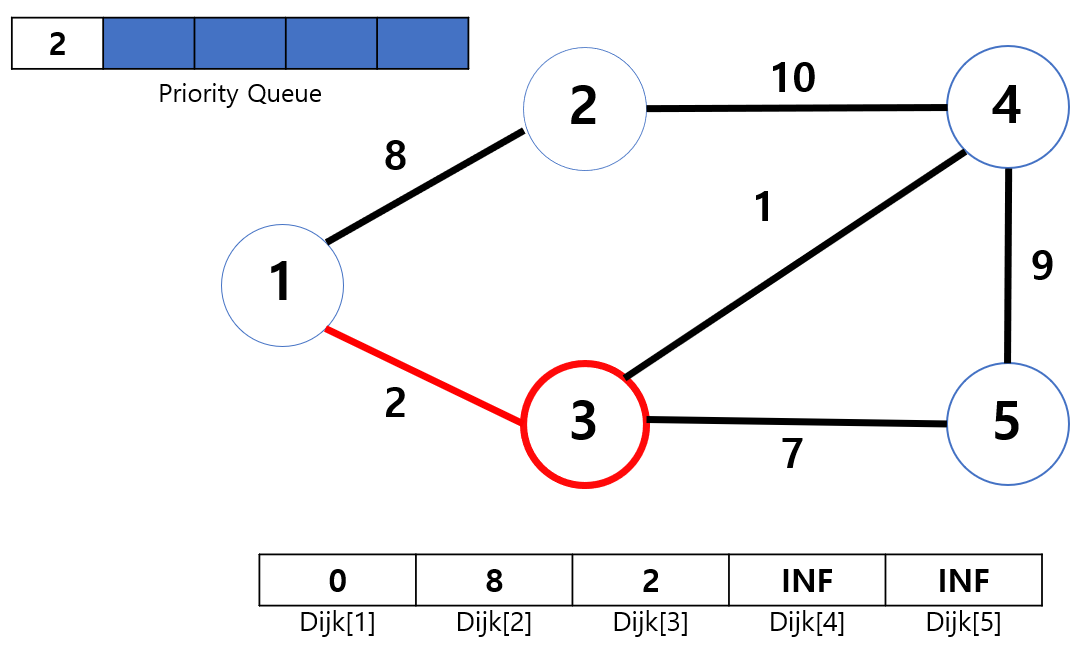
우선 3번 노드에서 어디로 갈 수 있는지 판단해 보겠습니다. 3 -> 1의 가중치는 2인데, 1번 노드까지 오면서 저장한 가중치(Dijk[3])는 0 입니다. 이 때 1번 노드로 이동을 하게 된다면 2(Dijk[3])+2(가중치)=4의 가중치를 소비하게 될 것입니다. 하지만 이 4라는 값이 Dijk[1]=0보다 크므로 이동할 필요가 없게 됩니다. 따라서 1번 노드로는 더 이상 이동하지 않습니다.
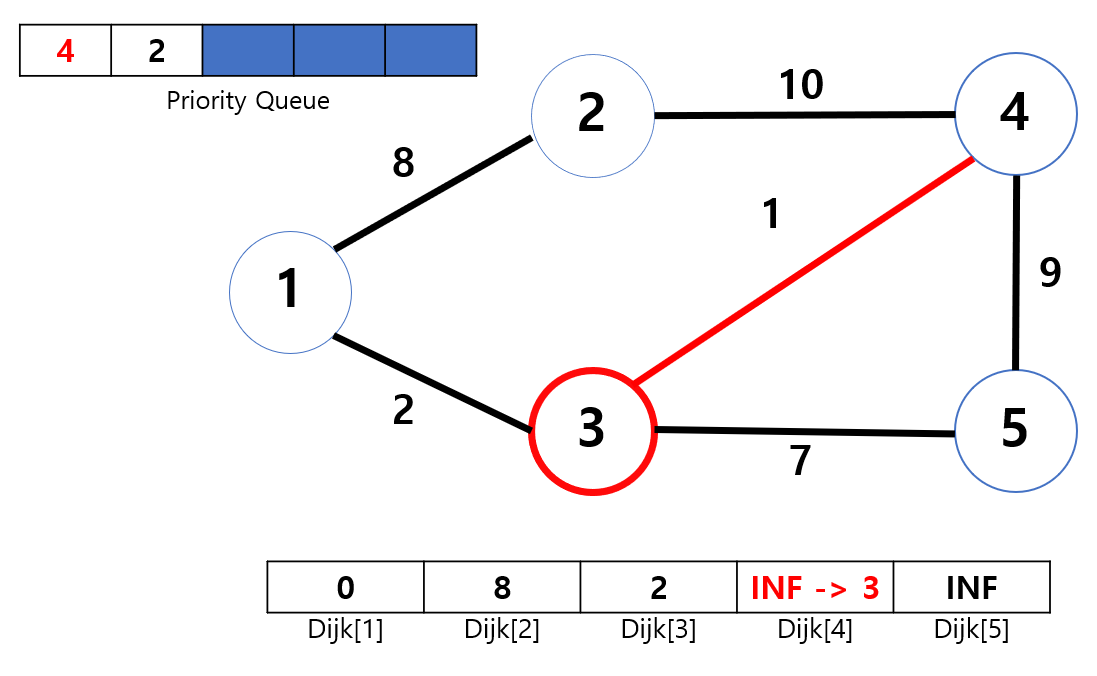
다음으로 3번노드에서 4번노드로 이동해 보겠습니다. 가중치 1인 간선을 선택해 3 -> 4 이동을 결심한다면, 2(Dijk[3])+1(가중치)=3을 부담하며 이동해야 합니다. 이 때, Dijk[4]는 INF로 3보다 큰 값이기 때문에 4번 노드로 이동할 수 있습니다. 이 때 4번 노드를 PQ에 삽입하면서 동시에 Dijk[4]=3으로 갱신해 줍니다. 동시에 PQ에서는 가중치 적은 값을 우선하여 정렬하게 되므로 4, 2 순으로 PQ에 위치하게 됩니다.
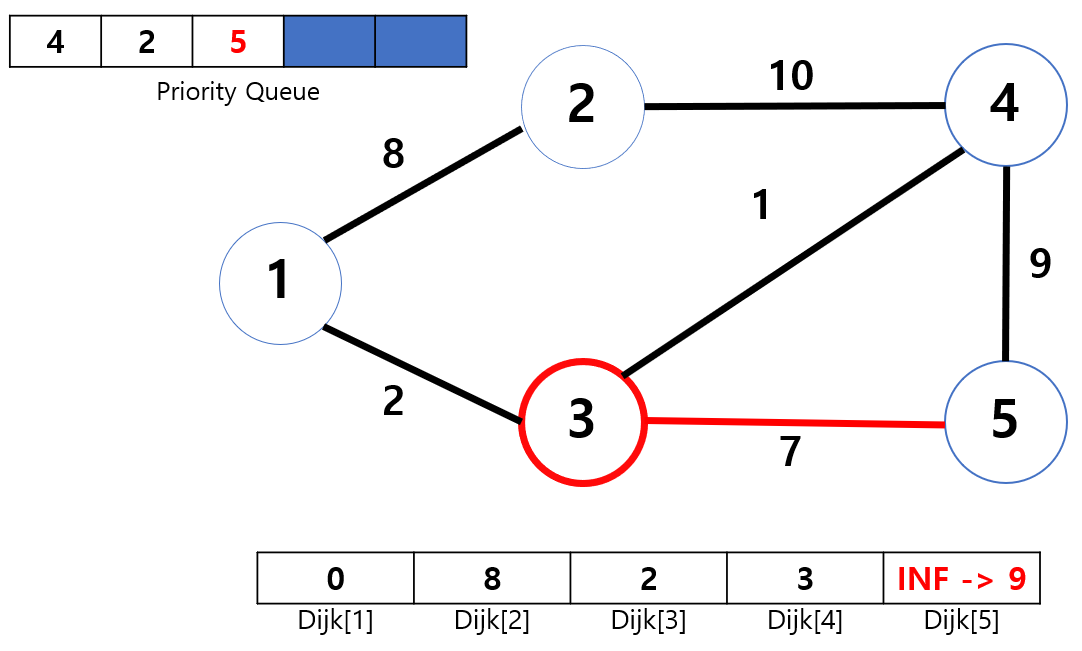
다음에는 3에서 5로 이동을 확인해 보겠습니다. 3 -> 5 이동하려고 보니 2(Dijk[3])+7(가중치)=9을 부담해 이동해야 하는데, 이미 저장되어 있는 Dijk[5]=INF가 9보다 큰 값이므로 충분히 이동할 가치가 있습니다. 3 -> 5 이동을 결심하면서 Dijk[5] = 9로 갱신하고 PQ에 노드5를 삽입해 줍니다. 동시에 PQ에서는 가중치가 가장 큰 노드5(가중치=9)를 맨 뒤로 보내면서 보관하게 됩니다.
이와 같은 방식으로 PQ 맨 앞 노드를 가져와 이동 가능한 다음 노드가 무엇인지 살펴보고, 그 노드의 Dijk값이 무엇인지 확인하며 갱신 가능하면 방문하는 순으로 반복적으로 수행해 줍니다.
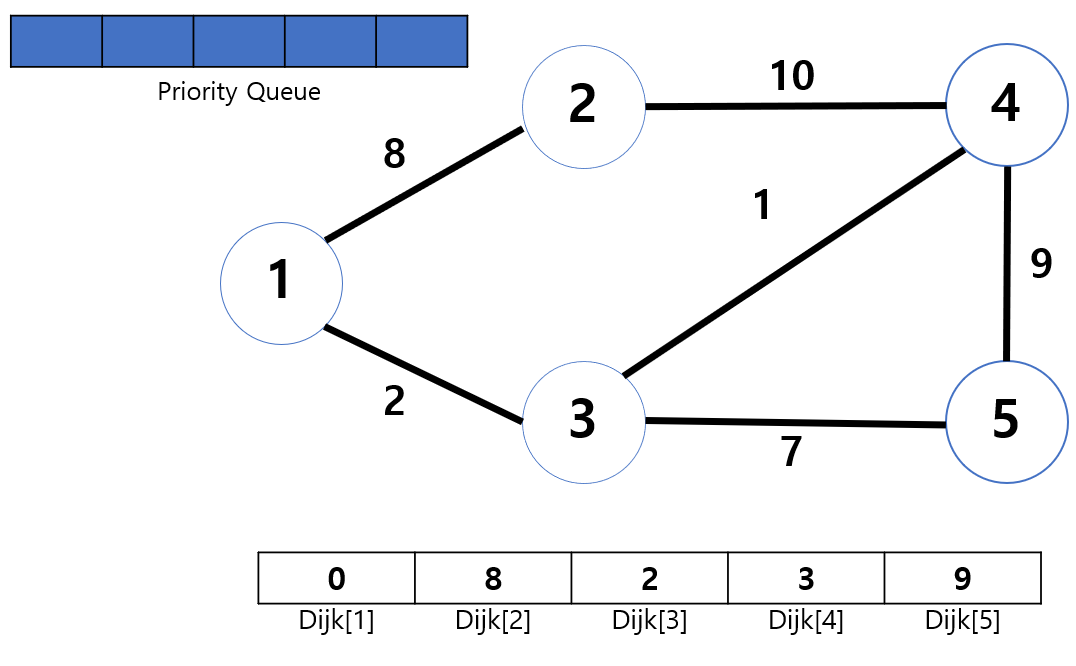
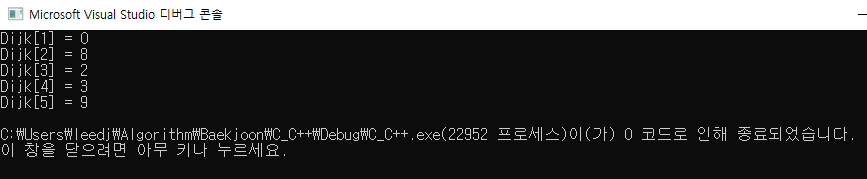
PQ에 들어있는 모든 노드들의 탐색전이 끝나 텅 비어있는 상태가 다익스트라 알고리즘이 끝난 상태이고, 이 때 저장되어 있는 Dijk 배열들의 각 값들이 그 결과를 보여줍니다. 다익스트라 알고리즘을 다시 백업해 보자면, 한 노드에서 다른 모든 노드까지의 최단 경로라고 앞서 말씀 드렸습니다. 그럼 Dijk 배열 각각에 저장된 의미는 다음과 같습니다.
Dijk[1]: 1 -> 1까지의 최단 경로
Dijk[2]: 1 -> 2까지의 최단 경로
Dijk[3]: 1 -> 3까지의 최단 경로
Dijk[4]: 1 -> 4까지의 최단 경로
Dijk[5]: 1 -> 5까지의 최단 경로
3. 음수 사이클에서의 다익스트라
음수 사이클을 가진 그래프에서는 다익스트라 탐색이 불가능 합니다. 음수 사이클을 가진 그래프 예시를 들어 확인해 보겠습니다.
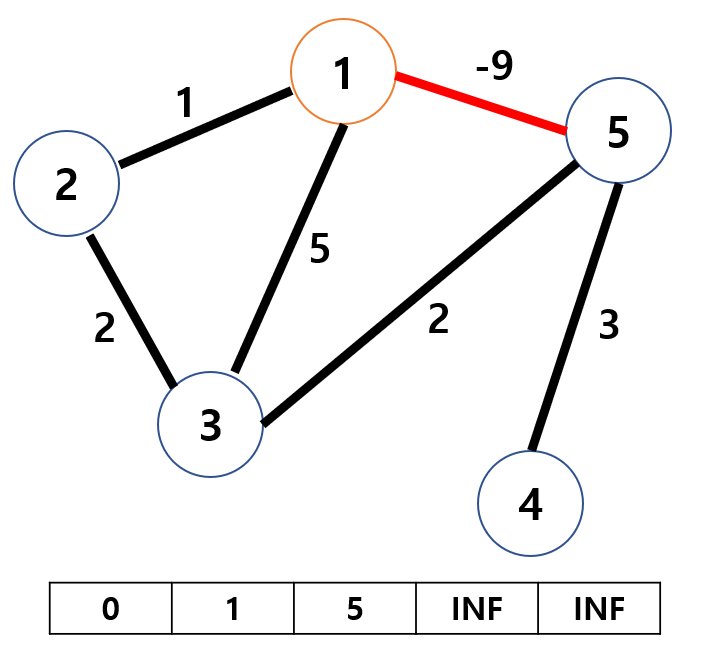
출발점이 노드 1이라면 노드 1부터 최소 비용을 탐색하게 되고, 노드 2와 노드 3 까지의 탐색이 끝난 상태에서 배열에 가중치의 합이 저장되어 있다고 가정해 봅시다. 노드 5로 가는 간선을 선택하게 되면 가중치 -9를 선택하며 INF 대신 -9를 저장할 것입니다.
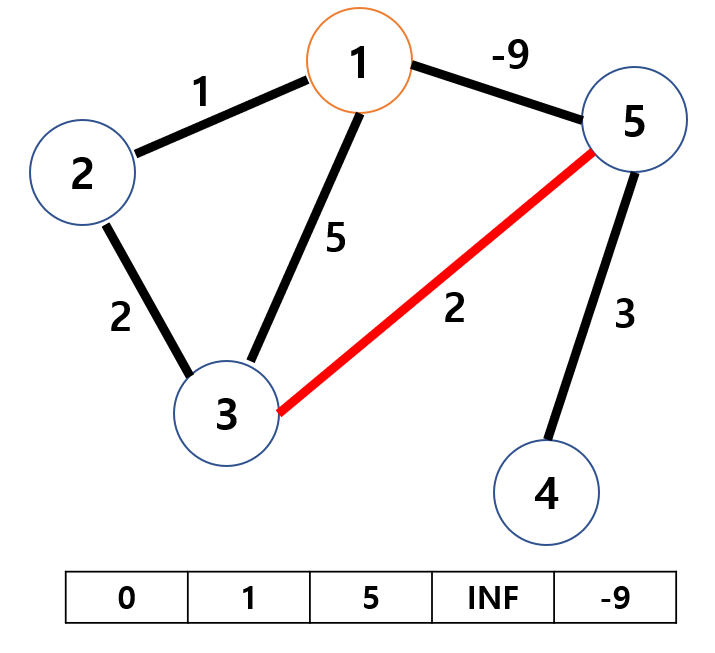
이제 노드 5에서 탐색을 시작하게 되어, 노드 3으로 이동해보려 하니 -9+2=-7로, 이미 저장되어 있는 5보다 작기 때문에 노드 3으로 이동이 가능합니다.
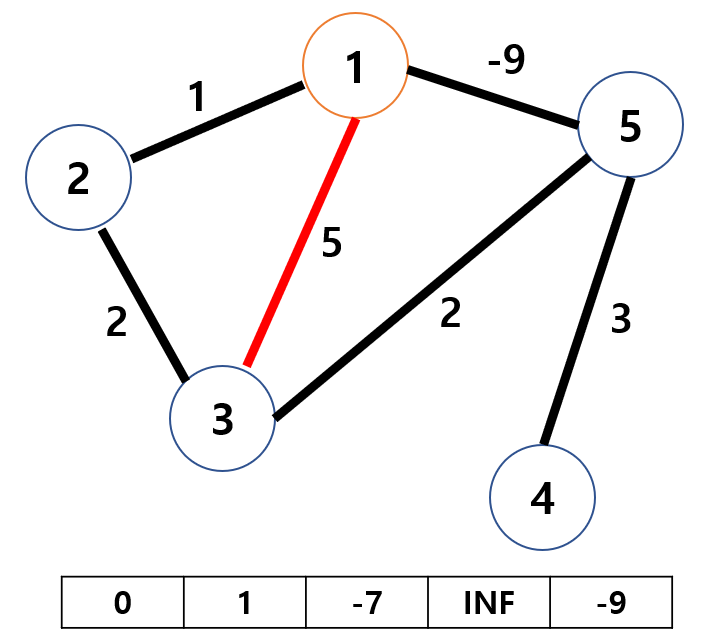
다시 노드 3에서 탐색을 시작하게 되고, 노드 1로 이동하려 하니 -7+5=-2로 이동이 가능해 노드 1로 이동합니다.
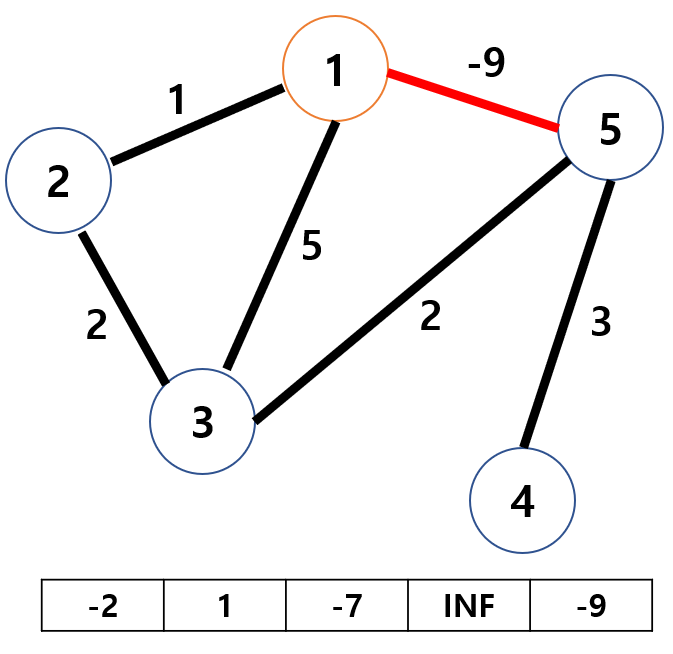
그 다음 스텝으로 노드1에서 노드 5로 갈수 있나, 다시 봐봤더니 -2+(-9)=-11로 이미 저장되어 있는 -9보다 작은 비용이기에 또 이동이 가능해 집니다! 이런 이유때문에 음수 가중치가 있는 그래프인 경우에 다익스트라 기법은 계속해서 돌고 돌아 무한대의 시간으로 탐색을 하기 때문에 활용할 수 없습니다.
4. 코드 구현하기
이제 배운 내용을 코드로 구현해 보겠습니다. 그래프의 형태(가중치 포함)는 위에서 설명한 예시를 그대로 재 활용해 보겠습니다.
1) 그래프 만들기
#include <cstdio>
#include <vector>
using namespace std;
#define INF INT_MAX
typedef struct {
int node; // 연결된 다음 노드 번호
int weight; // 간선의 가중치
}Data;
vector <Data> v[6]; // v[x]: x번 노드에 연결된 다음 노드와 가중치의 정보
void MakeGraph() {
// 1번 노드와 연결된 그래프 생성
v[1].push_back({ 2, 8 });
v[1].push_back({ 3, 2 });
// 2번 노드와 연결된 그래프 생성
v[2].push_back({ 1, 8 });
v[2].push_back({ 4, 10 });
// 3번 노드와 연결된 그래프 생성
v[3].push_back({ 1, 2 });
v[3].push_back({ 4, 1 });
v[3].push_back({ 5, 7 });
// 4번 노드와 연결된 그래프 생성
v[4].push_back({ 2, 10 });
v[4].push_back({ 5, 9 });
// 5번 노드와 연결된 그래프 생성
v[5].push_back({ 3, 7 });
v[5].push_back({ 4, 9 });
}
int main(void) {
MakeGraph();
}벡터를 활용해 a라는 노드와 연결된 노드 b, 그리고 그 사이 간선의 가중치를 담은 정보를 담아주며 그래프를 만들었습니다.
2) 최단 경로 값을 담을 배열 생성 및 초기화
int Dijk[6]; // Dijk[x]: x번 노드까지의 최단 경로 값
void InitDijkArray() {
for (int i = 1; i <= 5; i++) {
Dijk[i] = INF;
}
}
int main(void) {
MakeGraph();
InitDijkArray();
}
3) Queue 생성 및 시작 노드 정보 삽입/갱신
#include <queue>
typedef struct {
int node; // 연결된 다음 노드 번호
int weight; // 간선의 가중치
}Data;
struct cmp { // 사용자 정의 비교 함수
bool operator()(Data a, Data b) {
return a.weight > b.weight; // 가중치 오름차순
}
};
priority_queue <Data, vector<Data>, cmp> pq;
void InitQueue(int start) {
pq.push({start, 0}); // 시작하는 노드 삽입
Dijk[start] = 0; // Dijk[시작] = 0으로 갱신
}
int main(void) {
MakeGraph();
InitDijkArray();
InitQueue(1); //노드 1을 시작이라고 가정
}
4) Dijkstra 구현
void DijkStra() {
// priority_queue가 텅~ 빌때까지 다익스트라 알고리즘 반복 수행
while (!pq.empty()) {
// priority_queue 맨 앞 노드 가져오기
Data nowNode = pq.top();
pq.pop();
int node = nowNode.node;
int weightSum = nowNode.weight;
if (Dijk[node] < weightSum) continue; //이미 이전에 더 적은 가중치로 Dijk[node]를 갱신함
// nowNode와 연결되어 있는 다른 모든 노드 탐색
for (int i = 0; i < v[node].size(); i++) {
int nextNode = v[node][i].node;
int weight = v[node][i].weight;
// ( 다음 노드에 저장된 값 > 다음 노드로 방문하면서 소비할 가중치의 합 ) 일때만 값 갱신, 그리고 pq삽입
if (Dijk[nextNode] > weight + weightSum) {
Dijk[nextNode] = weight + weightSum;
pq.push({nextNode, Dijk[nextNode]});
}
}
}
}
int main(void) {
MakeGraph();
InitDijkArray();
InitQueue(1); //노드 1을 시작이라고 가정
DijkStra();
}
최종 코드
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
#define INF INT_MAX
typedef struct {
int node; // 연결된 다음 노드 번호
int weight; // 간선의 가중치
}Data;
struct cmp {
bool operator()(Data a, Data b) {
return a.weight > b.weight; // 가중치 오름차순
}
};
vector <Data> v[6]; // v[x]: x번 노드에 연결된 다음 노드와 가중치의 정보
int Dijk[6]; // Dijk[x]: x번 노드까지의 최단 경로 값
priority_queue <Data, vector<Data>, cmp> pq;
void MakeGraph() {
// 1번 노드와 연결된 그래프 생성
v[1].push_back({ 2, 8 });
v[1].push_back({ 3, 2 });
// 2번 노드와 연결된 그래프 생성
v[2].push_back({ 1, 8 });
v[2].push_back({ 4, 10 });
// 3번 노드와 연결된 그래프 생성
v[3].push_back({ 1, 2 });
v[3].push_back({ 4, 1 });
v[3].push_back({ 5, 7 });
// 4번 노드와 연결된 그래프 생성
v[4].push_back({ 2, 10 });
v[4].push_back({ 5, 9 });
// 5번 노드와 연결된 그래프 생성
v[5].push_back({ 3, 7 });
v[5].push_back({ 4, 9 });
}
void InitDijkArray() {
for (int i = 1; i <= 5; i++) {
Dijk[i] = INF;
}
}
void InitQueue(int start) {
pq.push({start, 0}); // 시작하는 노드 삽입
Dijk[start] = 0; // Dijk[시작] = 0으로 갱신
}
void DijkStra() {
// priority_queue가 텅~ 빌때까지 다익스트라 알고리즘 반복 수행
while (!pq.empty()) {
// priority_queue 맨 앞 노드 가져오기
Data nowNode = pq.top();
pq.pop();
int node = nowNode.node;
int weightSum = nowNode.weight;
if (Dijk[node] < weightSum) continue; //이미 이전에 더 적은 가중치로 Dijk[node]를 갱신함
// nowNode와 연결되어 있는 다른 모든 노드 탐색
for (int i = 0; i < v[node].size(); i++) {
int nextNode = v[node][i].node;
int weight = v[node][i].weight;
// ( 다음 노드에 저장된 값 > 다음 노드로 방문하면서 소비할 가중치의 합 ) 일때만 값 갱신, 그리고 pq삽입
if (Dijk[nextNode] > weight + weightSum) {
Dijk[nextNode] = weight + weightSum;
pq.push({nextNode, Dijk[nextNode]});
}
}
}
}
int main(void) {
MakeGraph();
InitDijkArray();
InitQueue(1); //노드 1을 시작이라고 가정
DijkStra();
}
6) 수행 결과
'Computer Science > Algorithm' 카테고리의 다른 글
| [알고리즘] 플로이드 와샬 - 최단경로 구하기(Floyd-Warshall), C/C++ (0) | 2022.03.28 |
|---|---|
| [알고리즘] 탐욕 알고리즘(Greedy Algorithm) (0) | 2022.03.15 |